[ML] Linear Regression

 

Linear regression : 데이터를 가장 잘 대변하는 직선을 구하는 것

 

Q : '데이터를 잘 대변한다' 는게 뭔데?

A : 예측값과 실제값의 차이가 크지 않은 것!!

 

Q : 그런 직선을 어떻게 구하는데?

A : 일단 지금 말한 것들을 식으로 만들어보자!!

 

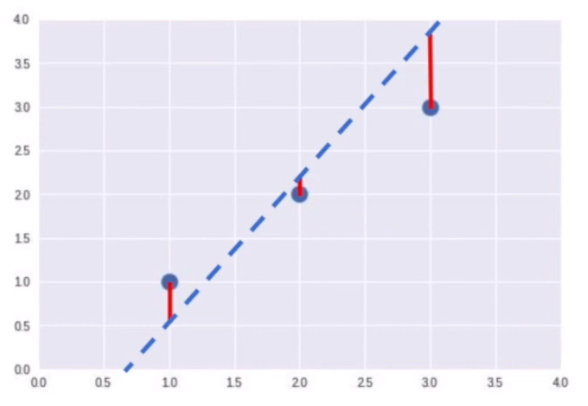
파란 점선 : Hypothesis (H(x)) = w*x + b

빨간 직선 : Cost (loss, error) = H(x) - y = 예측값 - 실제값

 

 

Q : 데이터를 잘 대변하는 직선을 만들기 위해서는 cost가 가장 작아야 하는구나!!

그럼 cost가 가장 작은 직선을 어떻게 찾아? 

A : 고등학교때 2차함수의 최솟값을 구할때 f(x)를 미분하고 어쩌구 했던거 기억나?

마찬가지로 f(x)를 정의하고 그걸 미분한걸로 cost가 가장 작은 직선을 구해볼거야!!

 

 

목적함수 f(x) = Cost function (비용 함수) = 각 cost들의 제곱을 평균낸 것

우리의 목적 : cost가 가장 작은 w와 b를 찾는 것

 

---

 

 

자!! 이제 f(x)를 정의했으니깐, 이 함수가 최솟값일때의 w와 b값, 그러니깐 데이터를 가장 잘 대변하는 직선의 기울기와 y절편 값을 구해보자!!

다양한 방법 중에서 가장 대표적인 Gradient descent algorithm(경사하강법)을 이용할거야!!

일단 이해하기 쉽게 b=0이고, w의 변화에 따른 cost 값의 변화를 그린 그래프를 참고하면서 설명해볼게.

 

결론부터 말하자면 이번 예시에서 데이터를 가장 잘 대변하는 직선은 y = x 야.

즉 w값이 1일때 오차(cost)가 가장 작게 나와야 할거야!!

 

그냥 눈으로만 봐도 w가 1일때 cost가 최솟값이지?

그런데 컴퓨터는 눈이 없으니깐 다른 방법으로 최솟값을 찾아야 해.

gradient descent 의 개념이 이제 나오는거야!

기울기(초록색 선)가 0에 가까워지는 직선의 x값이 함수의 최솟값이라고 판단하는건데, 그 순서를 보자.

 

 

첫 번째로 초기값을 지정해야하는데 이 값은 랜덤으로 주어도 좋아.

위의 그래프에서는 초기값(w)을 4로 주고 시작했어(y=4x).

그랬더니 기울기가 너무 크네? 좀 줄여야겠어.

 

 

그래서 두 번째로 cost값이 줄어드는 방향으로 w를 변경하는거야.

w를 얼만큼 변경하냐고? 

learning rate 값(α 값, 학습률)을 지정해주면서 학습을 얼마나 할지 우리가 결정하고, 그 값과 기울기를 곱한 값만큼 w에서 빼주면 돼. 식으로 나타내보자

 

w = w - 변화량(학습률 * 기울기)

 

 

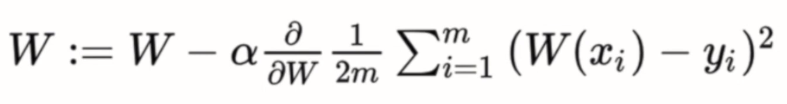
알파(α) 뒤에 있는건 cost fuction을 미분한 값인데 그게 기울기랑 똑같은거 고등학교때 배웠지?

아무튼 이런식으로 w를 변경하면서 마지막 세 번째로 cost 값이 최소일때까지 반복해주면 돼!!

 

 

이렇게 컴퓨터는 위의 함수에서 최솟값을 찾게 되었고, 

데이터를 가장 잘 대변하는 직선 식을 구하게 되었어.

 

 

** 주의

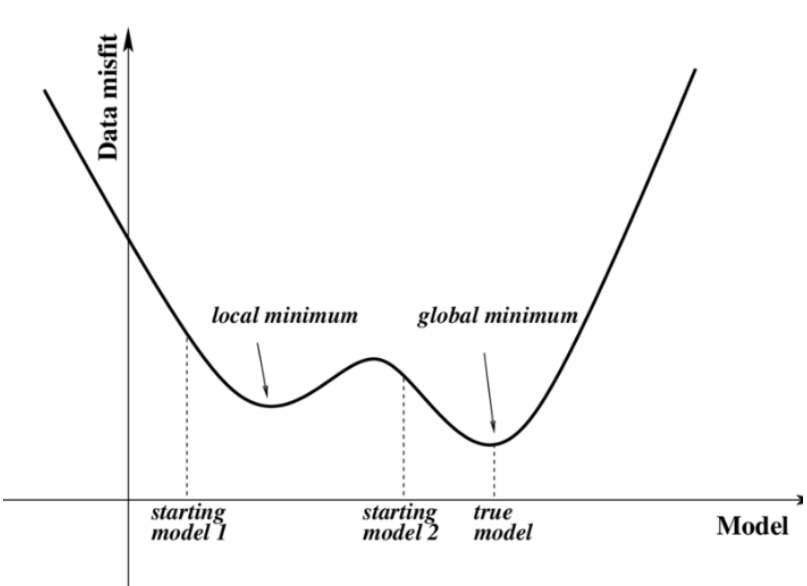
Gradient descent algorithm은 목적함수가 convex function이라는 보장이 있어야해!!

왜냐하면 구해진 최솟값이 local minimum 값일수도 있기 때문이야!!

https://www.researchgate.net/figure/Schematic-of-the-local-minima-problem-in-FWI-The-data-misfit-has-spurious-local-minima_fig1_267820876